3.2.10 Do clouds warm or cool the
earth?
Cloud layers of various types cover about half the surface area of the earth. Depending upon their thickness and the angle of incidence of the sun, a local cloud layer may reflect anywhere from a negligible fraction to more than half of the incident solar radiation back to space before it is absorbed at the earth's surface. Reflection by clouds accounts for about 2/3 of the solar radiation reflected back to space (i.e., 0.20 of the 0.30 planetary albedo). If the fractional cloud cover were to change (e.g., as a result of greenhouse warming), the albedo would change accordingly, in the same sense, and the fraction of the incoming solar radiation reaching the earth's surface would change in the opposite sense.
Clouds also contribute to the greenhouse effect. They absorb virtually all the upward infared radiation from below (even in the 'windows' of the absorption spectra of the gases) and re-emit it. The quantity of the upward re-emitted radiation is equivalent to what a black body would emit if it were at the same temperature as the cloud top. The colder the cloud top, the less radiation it emits to space and the more the layer contributes to the greenhouse effect. [By analogy, the warmer the blanket, the less heat it allows to escape from the bed, and hence the colder its own 'radiation temperature'.] The cloud top temperature is the same at the air temperature at the same level. Since almost all clouds reside in the troposphere, where temperature decreases with height, high (or thick) cloud layers tend to have colder tops and thereby contribute more to the greenhouse effect than low cloud layers. Surprisingly, the coldest cloud tops are found in the tropics, where deep convective clouds are able to penetrate as high as the 15 km (50,000 ft) level and spread out to form layers. We can estimate the cloud top temperature by taking a typical tropical surface ait temperature (say 30 C or 303 K) and subtracting the mean lapse rate of 7 C per km times 15 km, which yields -75 C or 198 K. Such high tropical cloud layers emit only about 1/4 as much infrared radiation as the earth's surface does.
Hence, it is apparent that cloud layers influence the surface temperature of the earth in two contradictory ways: they cool it, through their contribution to the planetary albedo, and they warm it, through their contribution to the greenhouse effect. Both effects are large, and it isn't clear which one dominates. However, one can infer that a high, relatively thin cloud layer of the cloud type called 'cirrostratus' would probably produce a net warming of the earth's surface, since it would make only a small contribution to the planetary albedo but, since even thin cloud layers are 'black' in the infrared, it could contribute substantially to the greenhouse effect. Conversely, a thick layer of low clouds like the layer of fog that blanketed Seattle on several of the mornings last week could substantially reduce the amount of solar radiation reaching the ground, while emitting nearly as much radiation in the upward direction as the underlying surface. (A layer of ground fog lying within a temperature inversion could even emit more, if its top were warmer than the underlying surface.)
On the basis of careful radiation measurements it has been determined that for the makeup of cloud layers present in the earth's atmosphere the cooling effect predominates over most of the earthis surface. The cooling is strongest over the regions of persistent stratus cloud decks off the coasts of Peru and Baja California and the southern Africa (on the Atlantic side)
Like the polar icecaps considered previously, clouds could constitute an important feedback mechanism in the climate system, but in contrast to the icecaps it could conceivably work in either direction, because we don't know whether an increase in temperature would result in an increase or decrease in cloud cover. Suppose that as the climate warms, the fraction of the sky covered by high (cold) clouds decreases, reducing the planetary albedo, but also allowing more infrared radiation to escape to space without absorption. To the extent that the latter effect predominates, the cloud-feedback upon the temperature would be negative: it would tend to make the climate less sensitive to changes in solar radiation (or greenhouse gases) than it would be otherwise. On the other hand, if global warming cause the fractional coverage of high clouds to increase, the effect would be just the opposite.
Thus far, our discussion of the energy balance of the earth and its atmosphere has been exclusively concerned with radiative fluxes. This narrow perspective made sense when we were dealing with the exchanges between the earth-atmosphere system and the rest of the universe. But when we apply it to energy changes within the earth-atmosphere system, we need to keep in mind that it is an artificial construct that we use just to help us understand the role of radiation. That's why we label the temperatures that we compute from the Stefan-Boltzmann Law as "radiative equilibrium temperatures". Wherever other modes of energy transfer (i.e., conduction, advection and convection) play a significant role, the actual temperature is likely to be quite different from the radiative equilibrium temperature. For example, if temperatures were strictly controlled by radiative transfer, much of the tropics and the summer hemisphere would be too warm for human civilization to thrive, and temperatures in the polar cap region would approach absolute zero every winter.
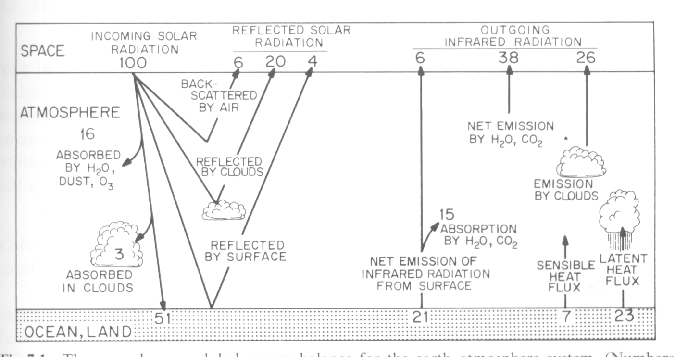
The globally averaged energy balance for the atmosphere and the earth beneath it (per square meter), based on actual observations, is shown in the above figure. You can think of it as being analogous to a picture of the personal finances of the average American wage earner, partitioned between the monet that's in the form of cash (the analogue of the atmosphere) and the money that's in the bank (the analogue of the underlying surface). Whether we're dealing with energy (or with money), it is often permissible to assume that the system is in a 'steady state' so that one need not take into account changes in energy storage, (or savings). In this case one can assume that incoming energy gains equal energy losses: (i.e., what is earned is spent).
If one were to construct such a budget for the average American wage earner, one would start by calculating his/her income, expressed as a rate, (e.g., dollars per month). A convenient way to do this would be to compute the total income reported to the Internal Revenue Service and dividing by the number of wage earners in order to express it as per capita income. The only "income source" for the earth is the solar radiation intercepted by the earth (1369 watts per square meter x pi R squared) divided by the surface area of the earth (4 p R2 ),which is equivalent to 1369/4 = 342 watts per square meter. Instead of representing it as energy units here, it is given a numerical value of 100%. Making this substitution is like represeting the averagr American wage earner's income as 100% or 100 units instead of, say $2.000 per month: it makes it easier to visualize the priorities in his/her budget. If you ever want to express it in actual currency units, all you have to do is remember that each unit is worth $20 per month. In the same manner, each unit in the energy budget is worth 3.42 watts per square meter
The next step in the calculation of the average Amercan's finances would probably be to deduct the part of his/her income that is not really disposable, like taxes and medicare, so as to be be able to focus on just the income that is disposable. Let's do the same for the earth by deduacting the fraction of the incoming solar radiation that is reflected back to space by air molecules (6 units), clouds and aerosols (20 units) and the earth's surface (4 units). The sum of these three percentages is equal to the earth's albedo (30 units).
Another 19 units of the incoming solar radiation is absorbed in its passage through the atmosphere: 16 in clouds and the remaining 3 in clear air by stratospheric ozone and tropospheric water vapor. The ozone specializes in absorbing ultraviolet radiation through processes that we will discuss next week, and the water vapor absorbs radiation in the near-infrared part of the spectrum where it has a number of strong absorption bands, as discussed in last Friday's lecture. The remaining 51 units of the incoming solar radiation reaches the ground, where they are absorbed.
The esrth's surface disposes of the solar radiation that it absorbs through a combination of infrared radiation (21 units), sensible heat flux (7units) and latent heat flux (23 units). Note that the combined energy losses by these three mechanisms adds up to the energy absorbed at the earth's surface (51 units).
The 21 units of infrared represents the net loss: i.e., the upward radiation from the surface minus the downward radiation from the atmosphere. The upward radiation can be computed from the Stefan-Boltzmann Law, using the observed surface temperature of the earth (288 K): it is 5.67 x 10-8 x 288 x 288 x 288 x 288 = 390 watts per square meter or 114 units, and the downward radiation emitted by the atmosphere is 93 units. That the earth's surface has to emit 114 units in order to get rid of 21 units testifies to the strength of the greenhouse effect. Of the 144 units of infared radiation emitted by the earth's surface 6 escape through the rather narrow 'windows' in the absorption spectrum.
The 7 units of "sensible heat flux" represents conduction of heat through the earth's surface and mixing through the lower atmosphere by dryconvection (i.e., convection that doesn't involve rainfall and the release of latent heat). The sensible heat flux tends to be concentrated in those areas where the earth's surface is much warmer (often by 10 C or more) than the overlying air mass; i.e., dry land areas on the sunlit side of the world and regions where cold air masses are flowing over warm ocean currents like the Gulf Stream (or even over Lake Washington on one of Seattle's rare cold winter days). These regions are often marked by bumpy air at low levels: the kind that can make landing a small aircraft just a bit uncomfortable. Over land such dry convection sometimes becomes organized in the form of small vortices called 'dust devils' that are often visible over eastern Washington on hot summer afternoons. The sensible heat flux that goes on within these isolated patches can sometimes locally exceed 100 watts per square meter, but when we average it over the entire globe, it is only around 7.
The 23 units of latent heat flux involves the hydrologic cycle in which evaporation takes place at the expense of the enenrgy that has been absorbed at the earth's surface, and the evaporation is realized within clouds in the atmosphere, often thousands of miles away from where the evaporation took place. The amount to latent heat flux transferred to the atmosphere is directly proportional to the amount of rainfall. To demonstrate this proportionality, we note that the average rainfall rate over the earth's surface is about 1 meter per year (just by chance coincidence, about the same as Seattle's annual rainfall). We can express this in terms of the amount of rain per day by dividing 1 meter per year by 365 days per year, which yields .00274 meters (or 2.74 mm) per day. The rainfall amount per second is .00274 m divided by 86,400 seconds per day, or 3.17 x 10-8 m (spread over a square meter) or 31.7 cubic mm, which is equivalent to one moderately large size raindrop.. That's not very much liquid water, but it represents a substantial amount of energy. To find out just how much, we convert it to kg of water by multiplying it by the density of liquid water, which is 1,000 kg per cubic meter and multiplying by the latent heat of vaporization,(2.5 x 10*6 joules per kg), which yields 91 watts per square meter. To express this in terms of the units in the diagram, we have to divide it by 3.42 watts per square meter per percent of the solar radiation incident on the top of the atmosphere, which yields 27 units: just a bit more than the 23 units in the figure. From this comparison we can conclude that the globally averaged rainfall must be just a bit less than a meter (23/27 meter, to be precise).
>From the numbers in the above figure, it is clear that the hydrologic cycle is a major player in the global energy balance. To appreciate its importance, one need only think about which is cooler on a hot, sunny day: a lush green lawn or bare ground (or pavement). The lawn is refreshingly cool, even though it may even have a lower albedo than the ground or pavement. It is cool because of the evaporation (or, strictly speaking, "evapotranspiration") from the grass, which transfers most of the absorbed solar radiation back to the atmosphere without requiring that the surface heating up the surface excessively, as is the case for conduction and heat transfer by the emission of infrared radiation. Plants such as trees and grass use evapotranspiration as a means of keeping cool on hot days, thereby evening out the large temperature extremes to which they are subject. In effect, they create their own "microclimates", which are more temperate than it would be in their absence. When vegetation wilts as it does during prolonged drought episodes, daytime temperatures soar: in the absence of latent heat flux, the surface stores the absorbed solar radiation until it becomes hot enough so that the combined net infrared radiation and sensible heat flux equal the absorbed solar energy. During the "dust bowl" summers 1934-36, afternoon tamperatures throughout large areas of the Great Plains reached values in excess of 110 F day after day. Such values are virtually unheard of except during severe drought. Hence, if, for any raeson (greenhouse warming, depletion of water supplies) the Great Plains were to turn into a desert or even dry grassland with sagebrush, the climate would change appreciably. In this sense, soil moisture in regions like the Great Plains constitutes another positive feedback in the climate system. that could be very important during summer.
Gases, unlike solid objects, don’t absorb and emit radiation at all wavelenghts but only in very specific wavelength regimes and some gases (like O2, N2 and the noble gases) hardly interact with radiation at all. The most important natural greenhouse gases are H2O, CO2 and O3. They are greenhouse gases because the atoms they are composed of are electrically charged and thus can be moved by the electromagnetic field. N2 and O2 are composed of identical atoms that carry no net charge. They cannot be moved by the elctromagnetic field and therefore have no effect on radiation, which of course excludes them from being greenhouse gases.
Three things can happen if an electromagnetic wave encounters a molecule of one of those gases:
Infrared radiation with relatively high energies (short wavelengths) can be absorbed and cause the molecule to vibrate. These vibrations require specific energies and only radiation with those energies can be absorbed by the respective gas. This causes the narrow lines in the absorption spectrum between 1 and 15mm.
Infrared radiation with higher wavelength has not enough energy to make the molecule vibrate, but it can cause the molecule to rotate if it gets absorbed by the molecule. Rotation can be caused by all the different infrared wavelengths above 20 mm, so the absorption sepectrum of the atmosphere seems continous there.
If the energy of the radiation happens to be such that it neither can cause the molecule to rotate or to vibrate then the electromagnetic wave just passes the molecule undisturbed as if it had not been there at all and can go directly out to space. These are the “windows” in the absorption spectrum: Wavelengths where the atmosphere doesn’t absorb at all.
Aerosols are small particles suspended in a gas. There are a lot of aerosol particles in the atmosphere, with a very variable concentration ranging from 1000/cm3 over the remote oceans to 100 000/cm3 in industrial areas. Most of these particles are too small to be seen: their sizes generally vary from <1nm to about 100mm.
This variability makes the atmospheric aerosol a part of the climate system that is not very well understood by now. But people believe that it is possible that aerosols cool the planet and cancel part of the greenhouse warming. In the lecture about aerosols I wanted to explain how aerosols could do that and why this issue is still in debate.
We will consider the effect of three different aerosol species: sulfate, soot and dust aerosols. Sulfate (SO4) is a white (nonabsorbing) salt, soot is the black residue from burning organic material (which absorbs strongly in the visible) and dust aerosol particles are microscopically small sand grains floating in the atmosphere, that are weakly absorbing.
Lifecycle of aerosols in the atmosphere:
Sources:
Aerosols get emitted into the atmosphere from antropogenic (man made)
and natural sources. For each of the aerosol species mentioned above I
list the major sources in the table below:
| Species | Antropogenic Source | Natural Source |
| SO4 | Industry: emits SO2 (gas), which is oxidized in the atmosphere to SO4 |
|
| Soot | Industry: Burning of fossil fuels
Traffic |
Forest fires |
| Dust | small | Deserts: Stand storms lift tiny sand grains high into the air |
Removal:
Aerosols don’t stay in the air forever. There are mechanisms to remove them, which are very dependent on particle size:
Small particles (diameter < 0.1mm): Those are small enough to get pushed around by molecules, so they move randomly through the atmosphere and diffuse to surfaces where they get stuck. The only surfaces available to them in the air are the bigger aerosol particles and cloud or rain droplets.
Large particles (diameter > 1mm): Those are too large to be moved by air molecules, but they are heavy enough to be pulled down by gravity and slowly settle towards the surface.
Medium sized particles: Neither of the above processes works very well so they tend to stay in the atmosphere much longer then the small or large particles. This is one of the reasons why they are most important for the climate. They finally get removed because of their role in cloud formation: When air ascends and cools it reaches a point where the water vapor condenses to form cloud droplets. But those droplets can only form on preexisting aerosol particles. Where it not for aerosol particles, there would be no clouds and the earth would look very different. If he cloud actually forms rain the aerosol particles contained in the rain droplets (and maybe some caught on the way) are removed from the atmosphere. This ‘wet removal’ process is less effective than the other two processes and so the residence time of the medium sized particles is about a week whereas the smaller and larger ones have a residence time of only some hours or maybe one or two days.
Aerosols and Radiation:
Aerosols interact with radiation and are therefore (like the greenhouse gases) important for the radiative transfer in the atmosphere. Because they are very small solid or liquid objects and they neither behave like gases nor quite like macroscopic objects. Most important for the climate of the earth is their interaction with solar radiation. In this respect they are different from most greenhouse gases, which mostly absorb infrared radiation (the only exception being Ozone, which absorbs also in the visible as we will learn later in this course). Aerosols can interact with radiation in two different ways:
1) All of them scatter solar radiation, which means they deflect the rays from their original direction without taking energy away from the beam. The direction in which most of the light is scattered by the particles depends on particle size:
Large particles normally make only small changes to the direction of the beam (we say they scatter in the forward direction). That means after an electromagnetic wave was scattered by a large particle it will most often travel as before towards the earth. So the large particles don’t make a big change in the incoming solar radiation and are not very important for the greenhouse effect.
Small particles scatter more or less like air molecules and among the millions of other air molecule they don’t make that big of a difference.
Again it is the medium sized aerosol particles that have the most effect: They scatter radiation in all directions and a considerable fraction back to space, so a lot of aerosol particles will increase the planetary albedo.
2) If an aerosol particle contains absorbing material (like soot) it will absorb radiation and get warmer just as a macroscopic object does. If a layer of the atmosphere contains a lot of absorbing aerosol particles it will warm.
Effects on climate:
Aerosols have various effects on climate because of their interaction with radiation and also because they are necessary for clouds to form which in turn interact with radiation. People distinguish the direct effect, which explains how aerosols change the climate by scattering and absorbing radiation themselves, and the indirect effect, which explains how aerosols could influence the climate by changing the optical properties of clouds. The effect is called indirect, because in this case it is the clouds that ultimately change the climate. Recently I discovered a so-called semi-direct effect in a paper that I will mention briefly.
Absorbing aerosols: absorbing aerosols still scatter some light
back to space, but they also absorb some sunlight and tend to warm the
layer of the atmosphere, where they are found. So they could have an overall
heating effect on the surface temperature, if they are close enough to
the surface and if their absorption is strong enough This is still in question,
because we don’t know enough of the absorption properties of atmospheric
aerosols!
Each trace constituent of the atmosphere, such
as water vapor has its own characteristic 'residence time' defined as the
time that the 'typical' molecule spends in the atmosphere. For water
vapor the residence time is the time required for a typical molecule evaporated
at the earth's surface to condense or freeze into liquid or solid form
in a cloud and return to the earth's surface. The time obviously
varies from one molecule to another: some enter into raindrops or snowflakes
almost immediately, while others may remain in the atmosphere for weeks
before they encounter an area of active precipitation. We can estimate
the average residence time simply by dividing the mass of water vapor in
the atmosphere by the rainfall rate (or the rate of evaporation, since
in the long term average over the entire surface area of the earth, the
two must be exactly the same). The numbers work out to about a week.
Note that if the water vapor molecules entered a queue as soon as they
evaporated from the earth's surface and waited their turn to condense out
of the atmosphere, then the residence time would be the same for all molecules
and it would be equal to the time computed from this formula.
The atmosphere is saturated with water vapor in clouds, where liquid water and water vapor co-exist in a state of near equilibrium. But throughout most of the atmosphere the air is unsaturated: i.e., it contains less than the equilibrium concentration of water vapor. A useful measure of the amount of moisture in the air is the 'relative humidity', defined as the actual concentration of water vapor molecules in the air divided by what the concentration would be in saturated air at the same temperature. Relative humidity in the lowest km of the atmosphere ranges from typical values of 10-20% over deserts, to 50% on a typical summer aftenroon in Seattle to around 80% in humid tropical air masses, to around 100% in areas of fog and rain.
The amount of water vapor in saturated air (air with a relative humidity of 100%) increases by about 2% for each 1 F increase in temperature: i.e., warm air can 'hold' more water vapor molecules (without having them condense out) than cold air can. Hence, we can change the relative humidity simply by changing the temperature of the air: we don't need to change the amount of water vapor in it. For example, relative humidity usually rises during the evening, when the temperature is dropping, and drops sharply on sunny mornings as the air warms up.
Scientists don't really know whether the distribution of relative humidity in the atmosphere would change in the event of a rise or fall in global-mean temperature, but a reasonable 'default assumption' that many have adopted (and seems to be borne out by most climate models) is that it would not change significantly: e.g., that humid tropical air masses would continue to have relative humidities around 80%. If that's true, then a global warming of, say, 1 F would be accompanied by a 2% increase in the amount of water vapor in the atmosphere. Since water vapor is one of the primary greenhouse gases, an increase in atmospheric water vapor concentrations would serve to enhance the greenhouse effect, thereby causing surface air iemperature to rise by an additional amount. This positive feedback increases the sensitivity of global temperature to changes in CO2 concentrations by a factor of x.x: i.e., an increase in CO2 sufficient to warm surface air temperature by 1 degree under the assumption that the amount of water vapor in the atmosphere remains constant will warm it by xx degrees if the water vapor is allowed to increase enough to hold the average relative humidity at a constant level. The water vapor feedback is much stronger than the ice-albedo feedback considered previously. In fact, were it not for the widespread belief in the existence of a strong water vapor feedback, greenhouse warming would not be considered nearly as serious a threat as it is.
Under the assumption of constant relative humidity, the amount of water vapor in the atmosphere increases exponentially with temperature, doubling for each 20 F temperature increase. Not only does the amount of water vapor increase with temperature, but the rate of increase with temperature ncreases as well. Hence, the warmer the temperature of the planet, the stronger the water vapor feedback and the more sensitive the temperature to changes in the concentrations of greenhouse gases. If it were warm enough, it is conceivable that the oceans could literally boil away, creating a massive atmosphere consisting mostly of steam. There is speculation that such a 'runaway greenhouse' might have occurred on Venus.
Some scientists have questioned the assumption
that global warming wouldn't change the distribution of relative humidity
in the atmosphere. They argue that in a warmer world, deep cumulus
convection in the tropics would be more vigorous. Among the possible consequences
of enhanced convection could be a reduction in the relatve humidity in
the upper troposphere. It might seem counterintuitive that an increase
in the volume of air carried aloft by buoyant updrafts could make the upper
troposphere drier, but this idea isn't as crazy as it sounds. The
updrafts in heavy showers and thunderstorms occupy less than 1% of the
area of the tropics: the remaining 99% is occupied by a more gentle sinking
motion which can be viewed as the 'return flow' in the convection cells.
This subsiding air is relatively dry (i.e., its relative humidity is less
than 50%) because it is warming (by compression) as it descends, like the
air on the lee side of a mountain range. If the convection were to
become more vigorous, it is not inconceivable that the sinking air in the
middle and upper troposphere could become even drier, allowing more of
the infrared radiation from lower (warmer) layers to escape to space without
absorption. It has been argued by some scientists that such a drying
could substantially reduce, or even reverse the direction of the water
vapor feedback. Whether this line of reasoning is difficult to judge
because it depends upon the details of the workings of moist convection
works, which are not well understood. The uncertainty with respect
to the strength of the water vapor feedback is among the most serious unresolved
scientific issues concerning greenhouse warming. It's one of the
reasons why not all scientists agree that greenhouse warming constitutes
a major threat.