In this lecture we consider only these most fundamental features
of the earth's climate:
the ones that don't depend on season, on the distribution of land and
sea, or on the
existence of mountain ranges. They depend only on the fact that
the equator-to-pole
contrast in incoming solar energy is stronger than the equator-to-pole
contrast in
outgoing infrared radiation (Fig. 5), and on the fact that the earth
is rotating.
We will consider how land-sea geometry and mountains modify this basic
picture
in the following lecture.

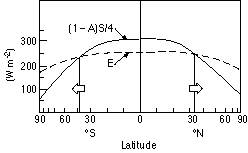
Fig. 4 Annual-mean incoming solar radiation and outgoing terrestrial
radiation as
a function of latitude. The latitude scale has been distorted
so that equal areas on
earth occupy equal widths.
To deduce what the climate of such a simplified 'earth like' planet
would look like
we rely on experiments that have been performed with numerical models
of the
atmospheric component of the climate system. When realistic land-sea
geometry,
mountains, and seasonal changes in solar heating are prescribed in
these models,
they yield quite realistic simulations of the observed climate.
Therefore the model
simulations of our idealized earth-like planet should have some credibility.
When such a model atmosphere is 'turned on', starting from a state of
rest (no winds,
horizontally uniform temperatures) the tropics warm and the polar regions
cool in
response to the imposed latitudinal contrast in the sun's heating,
which is prescribed
in a way that mimics that in the real atmosphere. Let's
assume that when the heating i
s first turned in, the atmosphere is not rotating. The
ensuing sequence of events is
depicted schematically in Fig. 5.
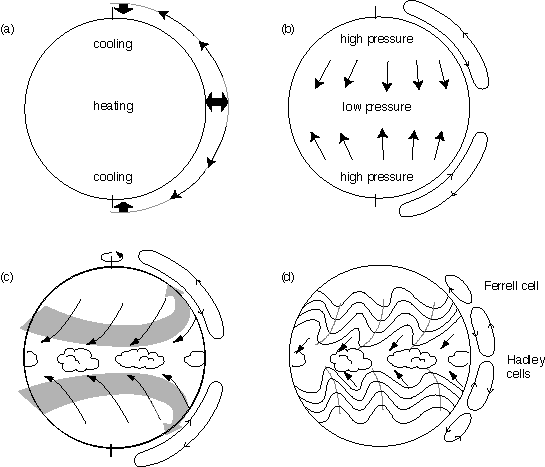
Fig. 5 Schematic depiction of the development of the
atmospheric circulation,
starting from a state of rest.
The equator-to-pole contrast in incoming solar radiation cause the tropics
to
warm and the high latitudes to cool. The temperature changes
are largest in
the troposphere, which extends to about 10 km. As the tropical
troposphere
warms, thermal expansion causes the air at the 10 km level to bulge
upward
relative to the cooling air at the higher latitudes, as represented
by the heavy
arrows in panel (a) of Fig.5. Hence, the mass of air weighing
down on the
10 km level increases in the tropics and decreases in high latitudes.
The uneven
weight of the air gives rise to a pressure gradient, which pushes the
air poleward,
as depicted in panel (a) of the figure.
The poleward flow of air in the upper troposphere causes air to
'pile up' at
the higher latitudes. The increasing weight of the overlying
air column causes
sea level pressure to rise at high latitudes, while the sea-level pressure
at low
latitudes decreases by an equal amount. The equator-to-pole contrast
in sea-level
pressure drives a compensating low level flow toward equator as depicted
in
panel (b) of the figure. Together, the poleward high level flow
and the low level
equatorward flow make up a giant circulation cell extending all the
way from
equator to pole, with rising motion in the tropics and inking at high
latitudes,
as shown on the right hand side of panel (b). We can imagine
that
the equatorial
belt, where the air in the cell is rising should be wet, and the polar
regions, where
air is sinking should be dry.
Now let's turn on the rotation and see what happens. Once the
atmosphere starts
to rotate, The conservation of angular momentum begins to generate
a component
of the flow that circulates around the earth's axis as shown in panel
(c). To understand
how this 'zonal' flow arises we can invoke the principle of the conservation
of angular
momentum. This conservation law tells us that if we view the
motions in a fixed
frame of reference (i.e., a frame of reference that is not rotating
with the planet-- like
observing a merry-go-round without being on it), the product of the
zonal velocity
times the radius is conserved. Hence, objects moving toward
the axis of rotation will t
end to rotate faster and faster, and vice versa, as illustrated in
fig. 6. To demonstrate
this idea on a (small) merry-go-round, position yourself on the
outer edge of it and get
it spinning as fast as you can. Then pull yourself inward toward
the center and note how
the rotation rate increases. The larger your mass in proportion
to the mass of the
merry-go-round, the stronger the effect. To apply the principle
of the conservation of
angular momentum to a rotating atmosphere we simply have to note that
the poleward
moving air at the 10-km level should begin to rotate faster than the
planet, and this excess
rotation will be viewed by observers on the planet as a westerly wind
component. In a
similar manner, the low level equatorward return flow should rotate
more slowly than
the planet, and this rotation deficiency should be evident to an observer
on the planet as
an easterly wind component.
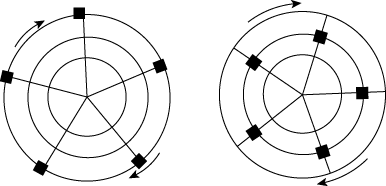
Fig. 6 Illustration of the conservation of angular momentum
as applied to a rotating
object with movable weights (denoted by the black squares).
We can get the same result by invoking the Coriolis force, which has
the following
properties: (1) it is directly proportional to the wind
speed on the rotation planet
(i.e., it affects only moving objects) (2) it is proportional
to rotation rate (i.e., to
have a Coriolis force, the planet has to be rotating (3) its
horizontal component,
which is what we care about, is proportional to the sine of the latitude
(i.e., it is zero
on the equator and increases with latitude) (4) it is directed
to the left of the wind in
the Northern Hemisphere and to the right of the wind in the Southern
Hemisphere.
We can think of the Coriolis force as deflecting the poleward flow
at the 10-km level
toward the right in the Northern Hemisphere (left in the Southern Hemisphere
to create a
westerly wind component and the easterly flow at the earth's surface
toward the left in
the Northern Hemisphere (right in the Southern Hemisphere) to create
an easterly
wind component.
As the heating in the tropics and the cooling at lower latitudes continue,
the
equator-to-pole temperature contrast gradually increases, and so does
the strength
of the upper level westerlies. The resulting circulation in panel
(c) resembles the
observed circulation in some ways (i.e., like the Earth it has tradewinds
and en
equatorial rain belt, but it has no midlatitude westerlies and the
deserts are in high
latitudes rather than in the subtropics. Does the model
have it wrong? No, we just
have to be patient.
After a few weeks of simulated time, the behavior of the model suddenly
changes.
At that point, the equator-to-poletemperature gradient reaches a critical
value
which is strong enough to support the development of extratropical
cyclones.
They develop as barely perceptible undulations in the westerlies, but
within a
few days of simulated time they intensify to the point where they begin
to change
the entire character of the flow by transporting heat, water vapor
and angular
momentum poleward. The specifics of how these changes come about
is beyond t
he scope of these lecture notes, but the overall effects are:
(1) the extratropical
cyclones become the primary mechanism for the poleward transport of
heat in
midlatitudes. Once they develop they prevent the further buildup
of the equator-to-pole
temperature gradient. Whenever the gradient gets too strong,
the storms intensify
and weaken it. (2) the extratropical cyclones disturb the upper
level flow in such a
way as to take angular momentum out of the tropics and deposit it in
midlatitudes.
This poleward transport of angular momentum is responsible for the
maintenance of t
he belt of westerly winds at the earth's surface in midlatitudes (3)
the extratropical
cyclones are responsible for the sinking motions in the subtropics
which favor desert
conditions and for a secondary maxima in rainfall around 55 N and 55
S shown in Figs. 2 and 7.
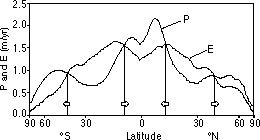
Fig. 7 Annual-mean incoming precipitation (P) and evaporation
(E) as a function of
latitude. The latitude scale has been distorted so that equal
areas on earth occupy equal widths.
Panel (d) of Fig. 5 depicts the atmospheric circulation as modified
by the extratropical
cyclones. Note how the equator-to-pole circulation cell in the
previous panel retreats
to the tropics. It is known as the 'Hadley cell'. The tradewinds
undergo a similar shrinkage
as a result of the development of the extratropical cyclones.
The desert belts separate the t
rades from the midlatitude westerlies. Note that Fig. 1 and Fig.
5d are virtually identical.