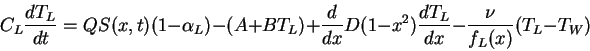
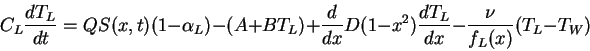
and
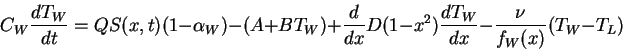
The subscripts L and W refer to land and water respectively. The model
represents a fraction of land at each latitude (![]() ), with the
remainder being ocean (i.e.
), with the
remainder being ocean (i.e. ![]() ).
). ![]() is the coupling
coefficient and changes how strongly the land and ocean temperatures
are tied together.
is the coupling
coefficient and changes how strongly the land and ocean temperatures
are tied together.
The standard set of parameters and functions for the model are the following:
Note that ![]() gives the adjustment time scale for land/ocean
in
gives the adjustment time scale for land/ocean
in
![]() . In this model the albedo has been parameterized a
little differently from the previous model, in order to account for
the differing albedos over land and ocean:
. In this model the albedo has been parameterized a
little differently from the previous model, in order to account for
the differing albedos over land and ocean:
We have also included the orbital parameters as quantities you can
vary. The values for the present day are:
Eccentricity, ![]() , = 0.01672
, = 0.01672
Obliquity, ![]() = 23.44
= 23.44![]()
Perihelion, ![]() = 102.07
= 102.07![]()
The eccentricity is the square root of one minus the square of the ratio of the major and minor axes. The obliquity is the tilt of the rotational axis relative to the orbital plane. The perihelion sets the phase of the seasons relative to the perihelion (or point of closest approach to the sun).
You should play around with all of these parameters to get a feel for what they do.
Option to include explicit sea ice
This sea ice model is a basic slab model with no leads, to match the simplicity of the EBM. We ignore the salinity of the sea ice in this model and assume all parameters are those of freshwater ice.
The net flux into the top ice surface is
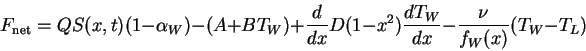
Finally we must make a special calculation anytime the ocean
temperature drops below -2
![]() , where we grow just enough ice to
bring the temperature back to -2.
, where we grow just enough ice to
bring the temperature back to -2.