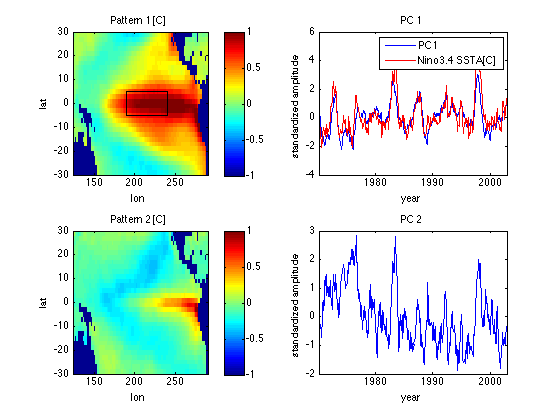
PCA of tropical Pacific monthly SSTA dataset (Jan 1970- Dec 2002)
Contents
- Load data
- Define dimensions
- Graphically time-step through it
- Do PCA using svd
- A more efficient way to compute leading SVD modes
- Extract leading space and time modes of variability
- Renormalize patterns and time series for easier interpretation
- Linearity
- Look if PDF of PC1 is multimodal (shows clustering)
- Now add plots for mode 2
Load data
clear
load SSTPac
whos
Name Size Bytes Class Attributes PSSTA 2520x396 7983360 double land 2520x1 2520 logical lat 2520x1 20160 double latmax 1x1 8 double latmin 1x1 8 double lon 2520x1 20160 double lonmax 1x1 8 double lonmin 1x1 8 double yd 1x396 3168 double
Define dimensions
nt = length(yd);
nlat = (latmax - latmin)/2 + 1;
nlon = (lonmax - lonmin)/2 + 1;
ns = nlat*nlon; % Number of spatial gridpoints
Graphically time-step through it
figure(1) clf for i = 1:nt PSSTAi = reshape(PSSTA(:,i),nlon,nlat); image([lonmin lonmax],[latmin latmax],PSSTAi','CDataMapping','scaled') xlabel('lon') ylabel('lat') axis xy title(num2str(yd(i))) caxis([-4 4]) colorbar getframe; % Used to force 'run' mode to spit out updated plot end
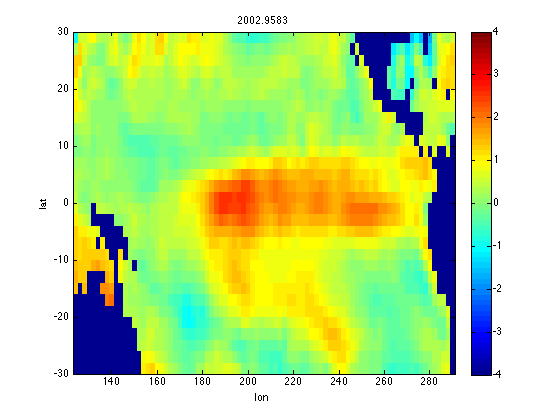
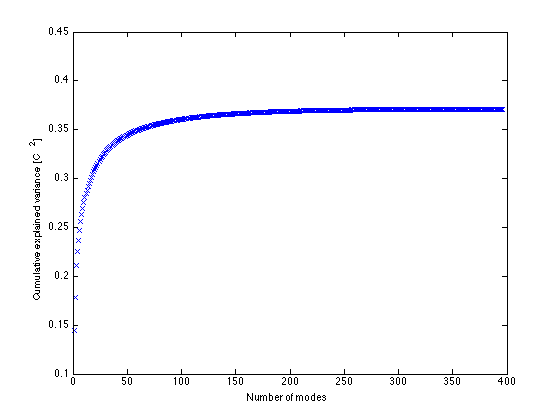
Do PCA using svd
% Remove the land points before doing analysis to avoid issues with NaNs. SST = PSSTA(~land,:); % Remove any residual time-mean at each location. SST = SST - mean(SST,2)*ones(1,nt); [U,Sigma,V] = svd(SST,0); % Always use 0 argument (economy SVD option) to % prevent possible massive unneeded computation. sizeU=size(U) % Since ns>nt this only gives the first nt columns of U, which is % thus nt x nt % Other columns would correspond to zero singular values sizeSig=size(Sigma) % Also, we only get the first nt rows of S, which is thus nt x nt. sizeV=size(V) % This will be the full nt x nt matrix in this case. s = diag(Sigma); % Vector of singular values % Plot cumulative variance explained by first k modes normsqS = sum(s.^2) % Show sum of SVs equals normsqSST = sum(SST(:).^2) % sum of squares of entries of SST plot(cumsum(s.^2)/(ns*nt),'x') % Divide by number of entries in SST % to plot a cumulative mean square variance xlabel('Number of modes') ylabel('Cumulative explained variance [C^2]') varfrac1 = s(1)^2/normsqS % Fraction of variance explained by modes 1&2 varfrac2 = s(2)^2/normsqS
sizeU =
2261 396
sizeSig =
396 396
sizeV =
396 396
normsqS =
3.7026e+05
normsqSST =
3.7026e+05
varfrac1 =
0.3892
varfrac2 =
0.0926
A more efficient way to compute leading SVD modes
% Note: For efficiency we can just compute the first two SVD modes as % follows - now U is ns x 2, V is nt by 2, and S is diagonal 2x2. [U,Sigma,V] = svds(SST,2); sizeU=size(U) sizeSig=size(Sigma) sizeV=size(V)
sizeU =
2261 2
sizeSig =
2 2
sizeV =
396 2
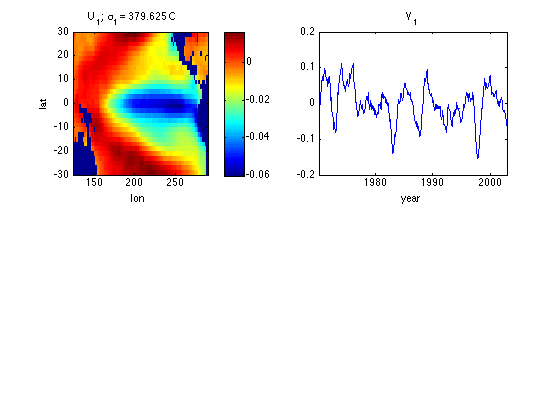
Extract leading space and time modes of variability
This code will work whether svd or svds was used to find U and V Columns of U give spatial patterns Columns of V give the corresponding time series Note each column of U, V has 2-norm of 1.
Uall = nan(ns,size(U,2)); Uall(~land,:) = U; U1 = reshape(Uall(:,1),nlon,nlat); % Turn column of U into a lat/lon % matrix including nan's at land points V1 = V(:,1); subplot(2,2,1) image([lonmin lonmax],[latmin latmax],U1','CDataMapping','scaled') xlabel('lon') ylabel('lat') title(['U_1; \sigma_1 = ' num2str(s(1)) ' C']) axis xy colorbar subplot(2,2,2) plot(yd,V1) xlabel('year') xlim([yd(1) yd(end)]) title('V_1')
Renormalize patterns and time series for easier interpretation
PC1 = -V1*sqrt(nt-1); % PC1 = V1 renormalized to have std=1 Ut1 = -U1*s(1)/sqrt(nt-1); % Ut1 = SST for PC1 = +1 std. % With 20-20 hindsight we also flip signs % of pattern and PC (which are ambiguous) % to match normal conventions. subplot(2,2,1) image([lonmin lonmax],[latmin latmax],Ut1','CDataMapping','scaled') xlabel('lon') ylabel('lat') title('Pattern 1 [C]') caxis([-1 1]) axis xy colorbar hold on % Add Nino3.4 region as a box plot([190 190 240 240 190],[-5 5 5 -5 -5],'k') hold off subplot(2,2,2) plot(yd,PC1) xlabel('year') ylabel('standardized amplitude') xlim([yd(1) yd(end)]) title('PC 1') load SSTA % SSTA = Nino 3.4 SSTA dataset from nino1.m; % also contains yr = corresponding decimal year inperiod = (yr>=yd(1)) & (yr <= yd(end)); SSTAN34 = SSTA(inperiod); R=corrcoef(PC1,SSTAN34); R = R(2,1) % Corr coeff of PC1 with Nino3.4 SSTA hold on plot(yr(inperiod),SSTAN34,'r') legend('PC1','Nino3.4 SSTA[C]') hold off % Note PC1 is very similar to Nino3.4 SSTA (see nino1.html), not % surprising since pattern 1 has a strong maximum loading in the Nino3.4 % averaging region of 120-170 W, 5S-5N.
R =
0.8243
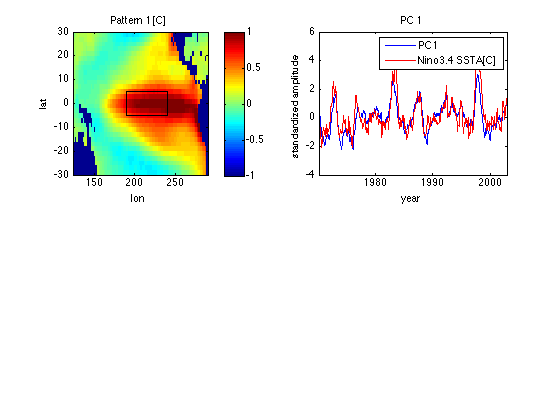
Linearity
% Compare patterns for strong positive and negative polarities of PC1, each % scaled to an equivalent PC1 = 1 pattern. ElNino = (PC1 > 1); LaNina = (PC1 < -1); SSTA_ElNino = mean(SST(:,ElNino'),2)/mean(PC1(ElNino)); SSTA_LaNina = mean(SST(:,LaNina'),2)/mean(PC1(LaNina)); UposPC1 = nan(ns,1); UposPC1(~land,:) = SSTA_ElNino; UposPC1 = reshape(UposPC1,nlon,nlat); % Turn column of U into a lat/lon % matrix including nan's at land points subplot(2,2,3) image([lonmin lonmax],[latmin latmax],UposPC1','CDataMapping','scaled') xlabel('lon') ylabel('lat') axis xy caxis([-1 1]) colorbar title('El Nino (PC1>1)') UnegPC1 = nan(ns,1); UnegPC1(~land,:) = SSTA_LaNina; UnegPC1 = reshape(UnegPC1,nlon,nlat); % Turn column of U into a lat/lon % matrix including nan's at land points subplot(2,2,4) image([lonmin lonmax],[latmin latmax],UnegPC1','CDataMapping','scaled') xlabel('lon') ylabel('lat') axis xy caxis([-1 1]) colorbar title('La Nina (PC1<-1)') % Slight spatial pattern nonlinearity is evident, esp. for La Nina phase.
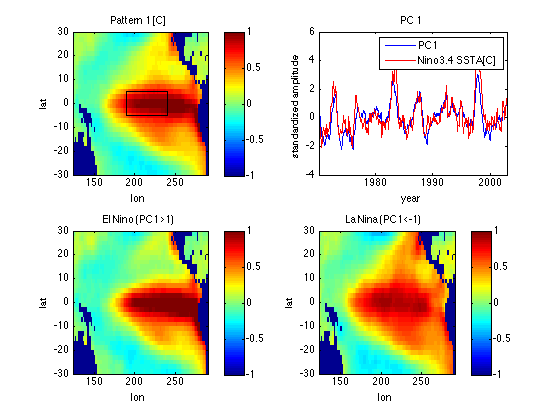
Look if PDF of PC1 is multimodal (shows clustering)
subplot(2,2,4) hist(PC1) xlabel('PC1') title('Histogram of PC1') % PDF of PC1 is slightly skewed but has a single main peak - no evidence of % clustering
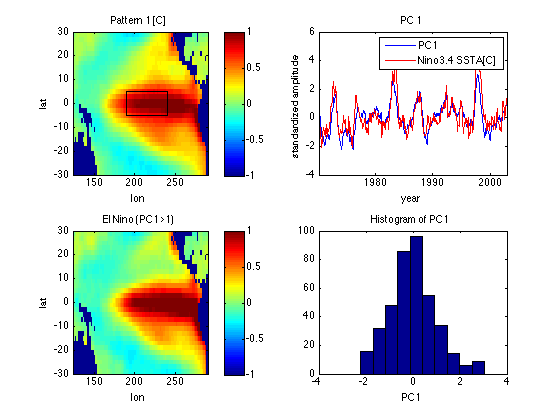
Now add plots for mode 2
U2 = reshape(Uall(:,2),nlon,nlat); % Turn column of U into a lat/lon % matrix including nan's at land points Ut2 = U2*s(2)/sqrt(nt-1); Vt2 = V(:,2)*sqrt(nt-1); % Renormalize V to have std=1 subplot(2,2,3) image([lonmin lonmax],[latmin latmax],Ut2','CDataMapping','scaled') xlabel('lon') ylabel('lat') title('Pattern 2 [C]') caxis([-1 1]) axis xy colorbar subplot(2,2,4) plot(yd,Vt2) xlabel('year') ylabel('standardized amplitude') xlim([yd(1) yd(end)]) title('PC 2') % Note patterns 1 and 2, and time series of PCs 1 and 2 are orthogonal.