Presentation given at the European Geophysical Society annual meeting, Nice, France, March 26, 2001. Small revisions Oct. 2002

Presentation given at the European Geophysical Society annual meeting, Nice, France, March 26, 2001.

Small revisions Nov. 2002.

When I researched this address, I found that I had been talking on this subject for over thirty (30) years. Aside from how old that makes me, it is embarrassing because I have been so ineffective in making my point.

To be sure, even I did not know what my point was for the first decade. But it became clear that if this theory is right, several other methods (K-theory, higher order closure (HOC), etc.) have problems.

The fact that the nonlinear equilibrium theory and its consequences have remained the same for several decades despite many challenges lends support to it being right. The theory has been expanded and checked by a generation of graduate students. Observations have supported the theory in general and never refuted it.

When I mentioned to my wife that I would be talking about Chaos, and expressed some problems with understanding what it was, she said to just take a look at my checkbook and compare my balance with that of the bank's. She of course was referring to the common definition of Chaos. Since I am going to invoke both meanings of this word, it is best that I start out with some definitions (in the first two overheads).

The common definition of chaos is succinct. The mathematical one is a bit nebulous. The PBL definition is probably influenced by my experiences. I will restrict my discussion to the coherent structure that arises from the nonlinear solution of the Planetary Boundary Layer (PBL) equations. Since I've done most of my work in the PBL my comments center on Turbulence and Chaos in the PBL. I suggest that ever since the presentation of the nonlinear PBL solution containing coherent structures explicitly as part of the PBL flow, a state of Chaos --- both definitions --- has existed in the PBL.

The existence of this new basic solution for PBL flow impacts PBL modeling, so let's look at the history of this impact --- or mostly a lack thereof.

I like to teach Ekman's solution to the Navier-Stokes equations. With Boussinesq's diffusivity constant, it is an elegant mathematical result that fits nicely into an hour lecture. All of these models listed on the slide are included in K-theory. In fact, Ekman initiated the variable K(z) studies. Also, note that Rossby & Montgomery initiated two-layer models with a mixing-length approximation for Ekman layer turbulence. This method is the basis of our PBL model at the University of Washington.

The fact that the Ekman solution was unstable to infinitesimal perturbations in most geophysical regimes emerged definitively in the '60s. Dissatisfaction with the myriad of K-theory schemes led to the nonlinear solution and the appearance of numerical solutions for the PBL by 1970. Expansion of the nonlinear instability theory to include the continuous spectrum has led to increased understanding of the fluid mechanics of this instability.

First attempts at similarity modeling were popular. Similarity parameters A and B were introduced as arbitrary parameters from dimensional analysis of the surface layer flow. The UW PBL model revealed that these parameters were functions of a single similarity parameter that appeared to be constant across large stratification changes.

Classical expansion techniques for closure of the viscous terms (HOC) was introduced. It fell from favor in classical fluid mechanics but has persisted in geophysics.

In the 80s, K-theories and numerical large eddy simulations (LES) were popular. The two-layer model linking a log-layer to an Ekman layer solution yielding a simple similarity solution was promulgated. In particular, an 'outer' solution that included the nonlinear solution led to the single parameter similarity solution with explicit formulas for the classical arbitrary (from dimensional analysis) constants (variables) A and B as a function of stratification.

While many important details of PBL flow were discovered in the 90s, reaffirming the nonlinear solution and the ubiquity of the Organized Large eddies (OLE), the basic large-scale modeling situation remained the same. Meanwhile, a revolution in large-scale PBL observations arrived in the form of global marine surface stress data from the satellite microwave sensors.

At the AMS 90^th anniversary meeting I attempted to delineate the difficulties with an 'evolutionary tree' of the equations used in various PBL modeling schemes.

Here, the divergent methods are clearly shown as they emanate from first assumptions. The Navier-Stokes equations emerge from both first-order closure and kinetic theory. However, since the expansion is not convergent in the singular region of the PBL, the higher-order closure equations are not as good as the N-S equations.

If we assume that Newton's law is valid for a small parcel of fluid in the PBL domain (Brown, Fluid Mechanics of the Atmosphere, Academic Press, 1991) then K-theory for SMALL eddies and a continuum hypothesis are valid. Then the nonlinear Ekman layer solution --- a modified Ekman profile containing explicit coherent structures --- and two-layer patching of this solution to a log-layer solution yielding a single similarity parameter model can be obtained. The ability of numerical models, including 'direct numerical simulation' models, to reproduce most of the analytic results was demonstrated by the 90s.

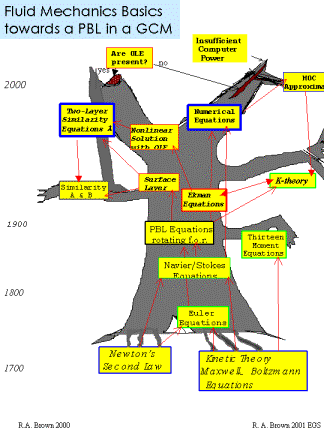
Signs of problems in boundary layer modelling are evident from the fact that fundamental questions have been published. When the nonlinear solution was offered it met with considerable resistance in numerical modeling circles. This is understandable --- while we start with Ekman's solution the first day, it takes most of the rest of a quarter to teach the nonlinear solution.

However, perhaps we should look at the this solution AND the basics of the flow equations --- the Newtonian fluid assumptions, the continuity assumption, and diffusion modelling requirements. Then we might realize that it is incorrect to use an eddy diffusion coefficient in a OLE environment unless the model resolution is very small (much better than any GCM). At least two books have been written on this problem (Brown, "Analytic Modelling of the PBL", Wylie & Sons, 1973; Stull "An Introduction to Boundary Layer Meteorology" (Concepts of Transilient turbulence) Kluwer Academic Publishers, 1988).

When GCM modelers realized this problem, observational proof of the solution was demanded, in particular to show the existence of OLE. The response to this request was weak in the 80s. Observations were not available except in special campaigns. We always found OLE and it conformed to theory, but the criticism was that we only looked in cold air outbreaks where the stratification produced a strong energy source. I will come back to this. But first we should look at the basic nature of the OLE to understand the problems. Then we can address the questions about the frequency of occurrence of OLE.

It is basically a problem of scaling in the equations and in measurement averaging. When a model function (MF) is constructed to relate a satellite sensor signal such as radar backscatter to a geophysical parameter such as wind, scaling enters the correlation construction. When data is used to establish the MF the averaging time is crucial. When a MF is used in an oceanographic or atmospheric application, the scale must be considered.The first procedure must be done well before the second can even be attempted. Both have potential for serious error if the true nature of the fluid flow involved is not fully understood. Sad to say, it often isn't.

All correlations involve measurements in the Planetary Boundary Layer (PBL). This is inherently a turbulent regime. The turbulence can only be represented by a proper average. However, there are other organized (coherent) flows in the PBL that are part of the mean flow on various scales and thereby removed from 'turbulence'. Typically, these involve geophysical eddies on scales from 100s of meters to tens of kilometers. Smaller scales can usually be lumped in with turbulence. Large scale turbulence can be averaged and parameterized in a 25-km footprint. This can also be done in an ad hoc manner for OLE. But it will vary with stratification, wind speed and sea-state. These numbers will also change as the footprint changes, as when a Synthetic Aperture Radar (SAR) 100-meter resolution is available the K(z) must change horizontally with position in the OLE.

The problems can be illustrated with a specific solution for a coherent structure in the PBL from the UW solution --- the OLE. Scatterometer model functions have typically been constructed by reference to a point source of data --- a buoy measurement. Let's look at the fundamentals of this measurement with a sketch of the solution with OLE (Rolls).

The rolls fill the PBL and produce an inhomogeneity that can lead to incorrect data comparisons. Consider measurements taken at stations A and B above. One is in the convergent/updraft region, one near the center and downdraft region.

The hodograph has the ratio, height/d (Ekman depth of frictional resistance) indicated --- the top of the PBL is at about 4-5 z/d. In each region of the rolls the hodograph is very different. At a point it will undulate or be steady depending on the OLE lateral movement.

In addition to atmospheric scientists, oceanographers must be concerned about the OLE. The hodographs are the same, and an oceanic PBL is used to illustrate the mean profile.

Note that the situation is complicated by the fact that the analytic solution for the OLE predicts they will move laterally with about 10% of the mean flow speed in neutral stratification. As convective energy increases, this lateral motion goes to zero. It is interesting that Jim Deardorff and I discussed why he wasn't getting the OLE in his numerical PBL model in 1971. They did try to appear, but were evanescent. Our conclusion was that, since we both had neutrally stratified, barotropic models, the numerical model would try to establish the OLE, but their lateral motion caused them to disappear. Unfortunately, this conversation wasn't published --- although the results were. They might explain why numerical models don't get OLE except in unstable stratification.

The problems in measurements are manifest in the search for a comparison data set to establish the empirical formulas for a satellite MF.

Consider the request for proof that the nonlinear solution with OLE is observed. Initially, the theory was inspired by the omnipresence of cloud streets, rows of clouds sitting on the top of the PBL as shown:

The data from the 70s consisted of a few airplane campaigns. The argument that these weren't conclusive proof for global PBLs was the observations were generally targeted at cold air outbreak regions where convective energy invariably produced rolls. The question was whether they appeared in the global ocean, that might be nearly neutrally stratified, This question was reinforced by the LES difficulties in obtaining OLE in neutral stratification.

The situation today is rapidly changing because of remote sensing data. These data have proven the ubiquitous existence of OLE. In addition they have stimulated PBL research by demanding a global 'surface truth' value of the surface winds in order to establish the satellite model functions.

In the 90s, observations by the SAR satellite sensors with microwave returns from resolutions of 100-m showed OLE effects appeared in the surface wind field (Johns Hopkins APL Technical Digest, vol 21, N 1, 2000). Subsequent surveys showed that evidence of roll imprints on the sea surface appeared 30% to 70% of the time in the North Pacific. Since the impact of the roll wind variation on the surface must be a special case, these numbers must represent a MINIMUM roll occurence.
Additional information from the NASA NSCAT scatterometer data suggested that the mean turning through the PBL was 19°, very close to the 18° predicted by the analytic model for neutral stratification. The angle of turning is also observed to change as predicted for thermal wind conditions.