Research - Under Construction

Madden-Julian Oscillation (MJO)

The Madden-Julian Oscillation is a near-planetary scale, slowly eastward propagating, intraseasonal tropical phenomenon; in plain English, it is a very large storm that starts in the Indian Ocean and moves eastward across the tropics over the course of several months. The exact strength and track of the storm vary, but the general features repeat with striking regularity.

Since it's discovery in the early 1970s (Madden and Julian 1971, 1972), a myriad of research has shown the importance of the MJO for weather and climate predictability. Observational studies have elucidated much of the structure of the MJO: horizontally it has a coupled Rossby-Kelvin wave pattern, with low-level convergence along the equator and alternating regions of dry and moist anomalies. Vertically, the MJO is characterized by narrow but deep convection, strong upward motion, and enhanced precipitation, coupled to a broad region of subsidence and supressed precipitation. These coupled regions propagate eastward together, resulting in the classic 'phases' shown below:

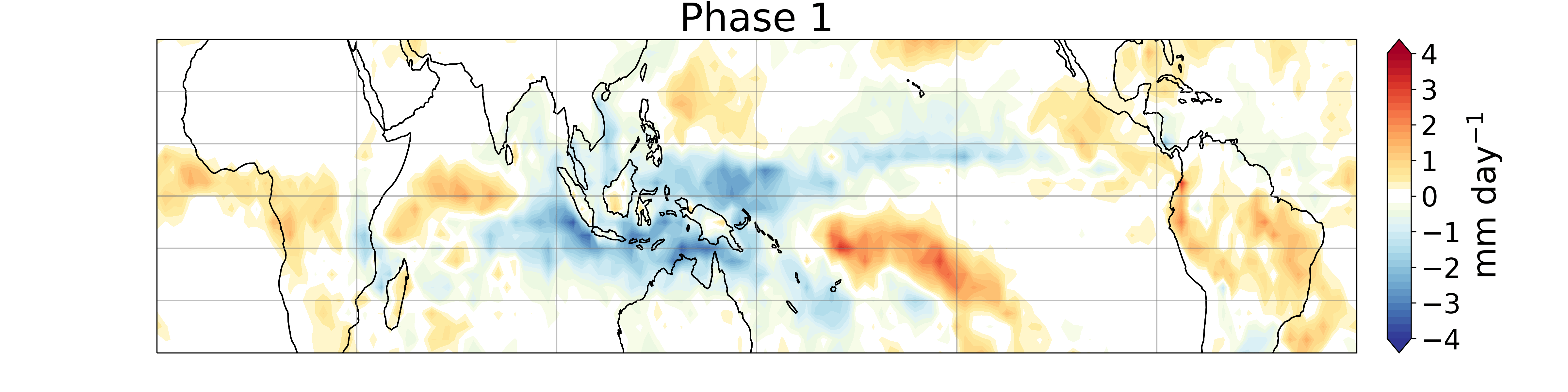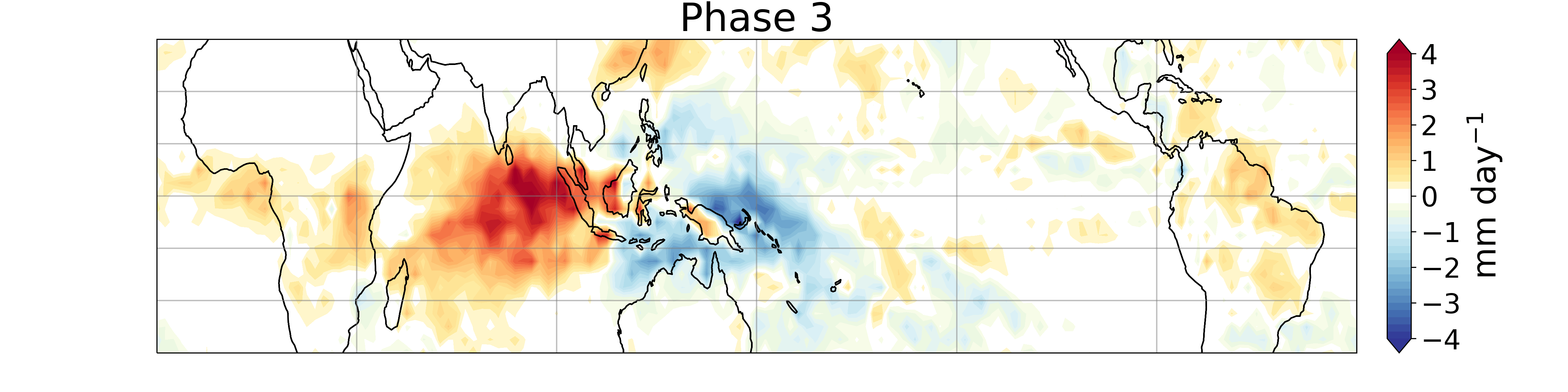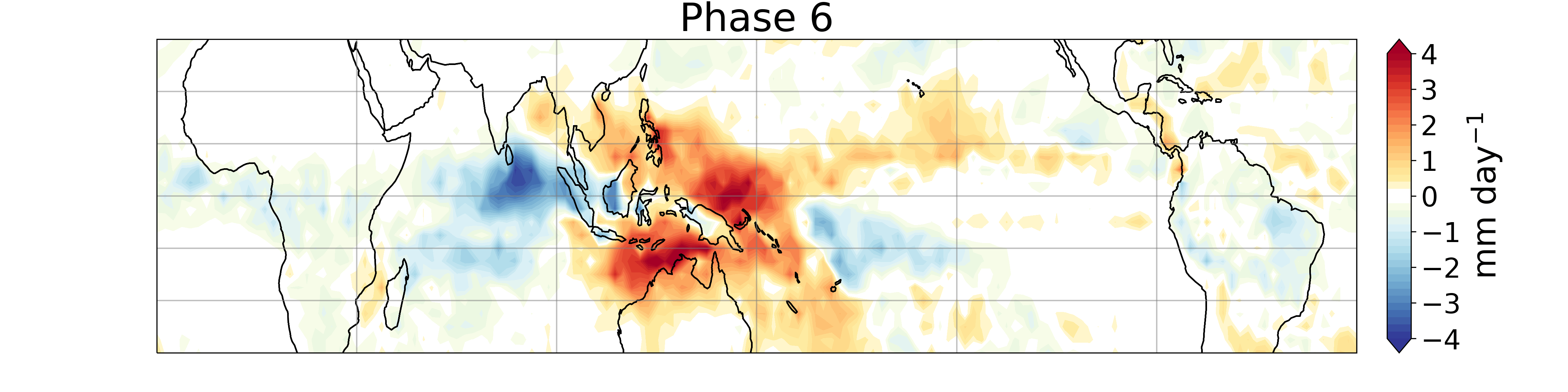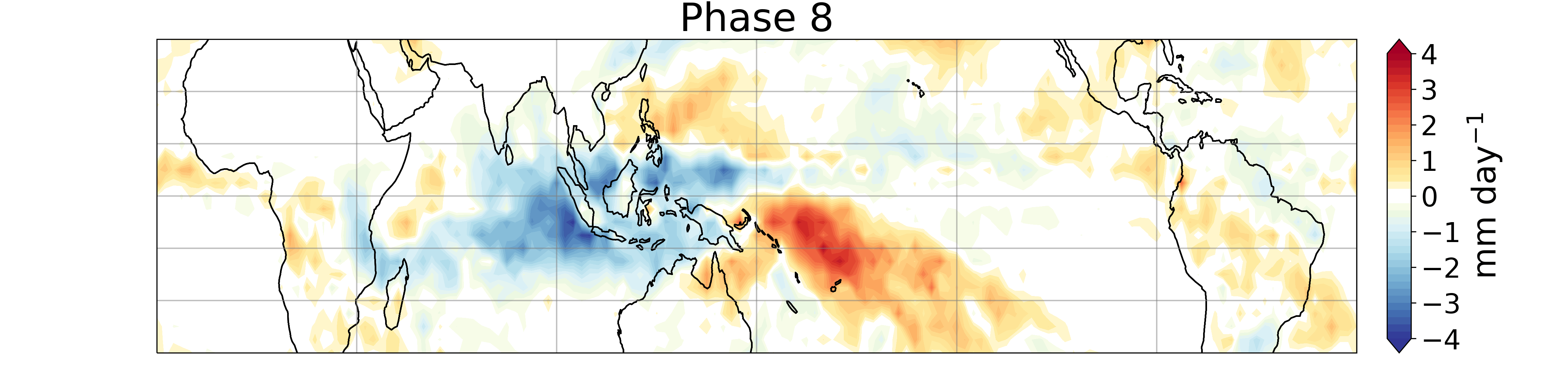
**Animation:** MJO-associated rainfall anomalies composited by MJO phase, as defined in Wheeler and Hendon (2004).

My research largely focuses on the models used to represent and study the MJO. In particular, linear analytic models have provided a powerful tool for improving our understanding of the physical processes that affect the MJO. Such models originate with the work of Matsuno (1966), which represented the dry tropical atmosphere using wave-like solutions of linearized governing equations on an equatorial β-plane. By including moisture as a prognostic variable and the effects of moist convection on the atmosphere, slow, eastward propagating modes emerge as model solutions. These MJO-analogs share many features with the observed phenomenon, but there is still room for improvement.

Model Setup

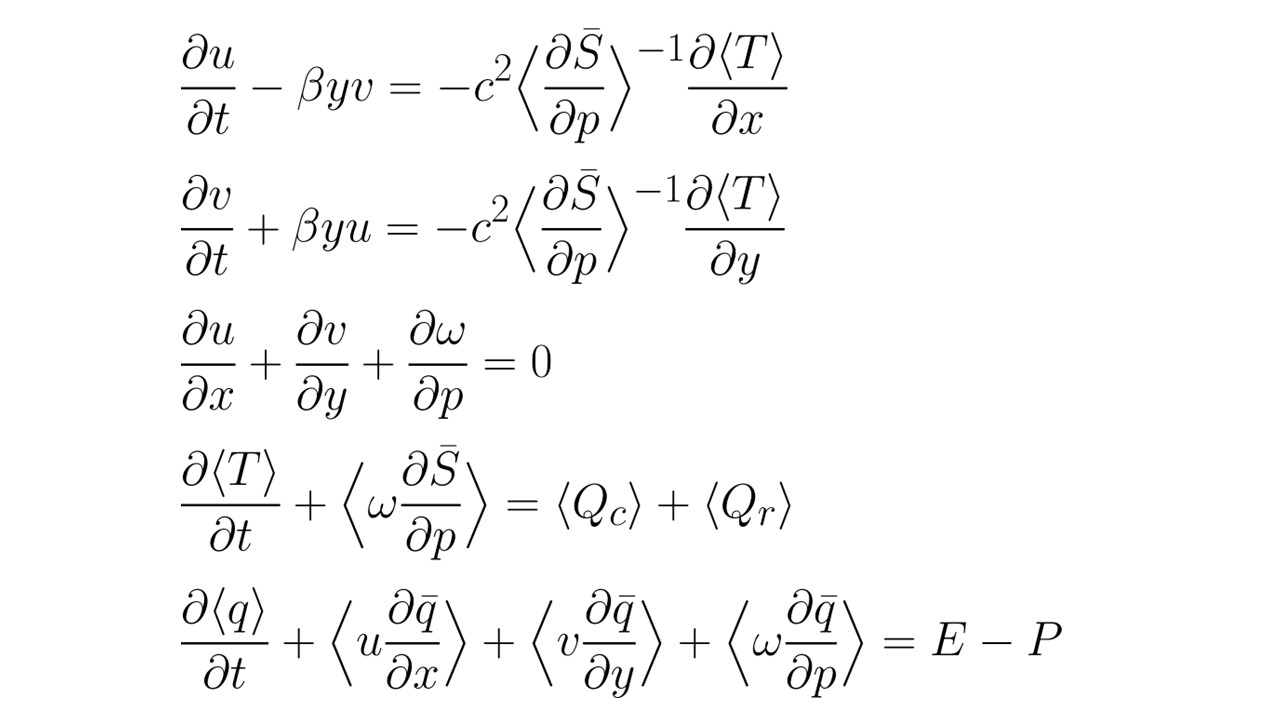
The basic model used in my research is a modified version of the model presented in Ahmed (2021). The tropical atmosphere is represented by a set of equations of motion linearized on an equatorial β-plane. The key model feature is the advection of mean moisture by the anomalous winds. As found in Ahmed (2021), the inclusion of zonal and meridional advection of mean moisture allows the equations to support a slowly eastward propagating mode with growth at the largest scales - an MJO analogue. The wave solutions are also destabilized by convective and radiative heating anomalies.