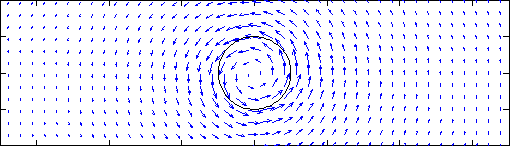
Consider a Rankine vortex as shown below. Outside the vortex boundary (indicated by the blue circle), the tangental velocity drops off with distance from the center like 1/r, while inside it increases linearly with radius.

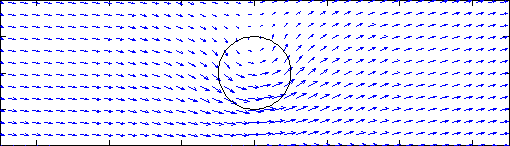
Now, let's superimpose a uniform flow from the left onto the vortex where the flow speed is the same as the maximum tangental speed of the vortex.  The vorticity normal to the plane of the flow is uniform inside the circle and zero everywhere outside the circle.

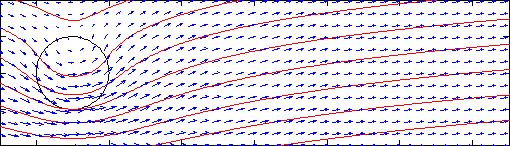
Finally, let's look at the streamlines for this combined flow (in red):

Now, let's put this flow into motion and follow the trajectories of three fluid particles.