Intro & Policies

Temperature Measurement
- Instructions
- Notes

Pressure, Humidity, and Precipitation
- Instructions

Weather State Analysis
- Instructions
- Notes

Wind Measurement
- Instructions
- Notes

Printer-Friendly Labs

Linear Regression

Linear regression is a method for determining the best linear relationship between two variables X and Y. If variables X and Y are uncorrelated, it is pointless embarking upon linear regression. However, if a reasonable degree of correlation exists between X and Y then linear regression may be a useful means to describe the relationship between the two variables.

Most analytical software packages (e.g. Excel, Matlab, IDL) have tools to compute linear regression. The usual approach is to use the least-squares method, which minimizes the squared difference between the actual data points and a straight line.

Let [x_i,y_i], i = 1,2,3,….,N be the N pairs of data values of the variables X and Y.

The straight line relating X and Y is y = mx + c, where m and c are the gradient and constant values (to be determined) defining the straight line. Thus, y(x_i) - y_i is the difference between the line and data point i (see Fig. 1). Taking all the data points, we seek values of m and c that minimize the squared difference SD.

SD =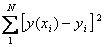

This is achieved by calculating the partial derivatives of SD with respect to m and c and finding the pair [m,c] such that SD is at a minimum. See Chapter 15 of Numerical Recipes by Press et al., Cambridge University Press, 1992 for full details.

Figure 1: Illustration of linear regression. For linear least squares regression, the idea is to find the line y = mx + c that minimizes the mean squared difference between the line and the data points (circles).

The result is that expressions are found for the values of m and c that minimizes SD. Analytical software packages will output these values (often termed the slope and the intercept). In addition, the least squares method allows one to estimate the uncertainties in the derived values of m and c, together with the correlation coefficient r (-1 < r < 1) that describes the degree of correlation between X and Y. These uncertainties are essential information that allows the user to determine how well the straight line fit really represents the relationship between X and Y given that you only sampled a small part of the population. The errors in m and c are usually given in the form of standard errors [wiki, “standard error”], i.e. σ_m and σ_c. In other words, the probability that the true value of m falls within the range m - σ_m to m + σ_m is approximately 67%.

Example

You have performed a least squares regression using Excel and estimated the slope and intercept of the relationship y = mx + c. The values Excel produces are m = 10.2 and c = 1.5 with standard errors σ_m = 3.0 σ_c = 2.0. What can you deduce about the value of the intercept?

The probability that the true value of the intercept is in the range 1.5 - 2.0 to 1.5 + 2.0 is approximately 67%. Thus, there is a reasonable chance that the intercept is actually zero, because the estimated range spans zero. Always be sure to quote the errors because these are required to understand how well the linear relationship really represents the relationship between X and Y. For example, if the error in the slope is also larger than the slope itself, then we really cannot be sure that there is a linear relationship at all.