Temperature lab: Some additional notes to help with the analysis

In this first detailed lab, students often have trouble applying the theory in lecture notes to the practical problem. These extra notes are intended to alleviate that problem.

Hg thermometer calibration: In the regression, T_true = 0°C, 100°C

Use T_true= aT_Hg + b to get a straight line fit. This will give errors s_a and s_b, so you quote the straight line fit in your report as:

T_true= (a ± s_a) T_Hg + (b ± s_b)

With the ASTM calibration, you should have 5 temperatures and three measurements at each temperature. A straight-line fit of TASTM vs. THg should give you an equation that you quote in your report as:

T_ASTM = (c ± s_c) T_Hg + (d ± s_c)

To see if the two-point fit and ASTM fit are in agreement compare the slopes (or “gain biases”) a and c and their errors. Also compare the “zero offsets” b and d and their errors.

Calibration of the other thermometers: You will have

where T_obs = the observations for each thermometer (Hg, Davis, bead thermistor, thermocouple).

You can use linear regression to get the fit in each case. However, T_ASTM is not quite the “real” temperature; it is related to the real, absolute temperature via the NIST-traceable calibration certificate data for the ASTM thermometer, i.e.,

You can obtain this calibration function by linear regression.

To get an estimate of the “total variance” on T_NIST, you can look at the average ASTM temperature, 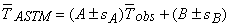, where the grand average of observations is

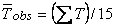
for a total of 15 measurements.

We can also get a standard error on the ASTM temperature from the “combination of errors formula” applied to (1), i.e.,

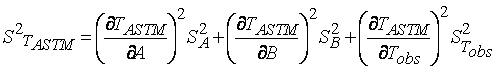(3)

From (3) and (1):

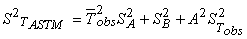(4)

We can get S_A² and S_B² from the regression analysis. We can get SOMETHING, the average error on the observations, from the standard error on the five mean observations:

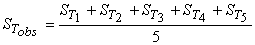
recalling that the error on the mean temperature at each point is SOMETHING where n = 3 if there are 3 measurements at the point.

Now if we look at the NIST calibration for the ASTM thermometer and the linear fit given by (2), we can use the same technique to calculate the variance in the NIST temperature, i.e. in the “real” temperature:

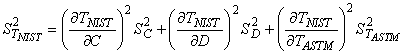(5)

Evaluating the partial derivatives, we have:

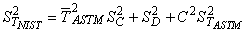(6)

Here 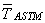is the average of the (fifteen) samples from the ASTM thermometer. So the solution technique is to get 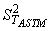from solving (4) and then to solve (6) to get an estimate of the error in the NIST temperature.

In a report, you can present results succinctly in a table. From looking at the error estimate, 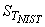, the thermometers can be ranked best to worst, e.g.

THERMOMETER	R2	Slope, A	Intercept, B (°C)	Slope Error	Intercept Error 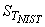(°C)	(°C)	Rank
Mercury
Davis
Bead Thermistor
Thermocouple
PRT