Intro & Policies

Temperature Measurement
- Instructions
- Notes

Pressure, Humidity, and Precipitation
- Instructions

Weather State Analysis
- Instructions
- Notes

Wind Measurement
- Instructions
- Notes

Printer-Friendly Labs

Sampling Error

In meteorology, as in many sciences, parameters of interest need to be treated statistically. For example, the air temperature at the surface fluctuates in space and time due to turbulent eddies and other transient phenomena. In order to estimate the mean temperature over some time and space interval, we make a set of measurements at different times (and perhaps different locations) and then combine these measurements to obtain an estimate of the mean temperature. The set of measurements we make is called the sample, which is taken from the entire population (the temperatures at all locations in space and time within our interval). Assuming that each measurement is unbiased, then the mean of the sample will be an unbiased estimate of the mean of the population, i.e. the desired quantity.

Let x_i be the sample values, where i = 1,2,3...N. The sample mean is given by

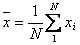[1]

We can also make an estimate of the error in the mean due to our poor sampling of the population, assuming that the measurements of x are unbiased. The sample standard deviation s is given by

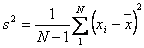[2]

Clearly, if the N measurements are all very close, then the error in the mean will be small. The error in the mean is given by 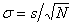. Therefore, if the sample has a given spread (i.e. a given s), then more measurements (greater N) leads to a smaller error in the mean.

Example

The wind speed u is measured at a particular point 5 times. The sample of measurements is 5.2, 5.4, 4.8, 6.1, 5.5 m s^-1. Estimate the population mean, and the error in this mean.

The estimate of the population mean is the sample mean, i.e. 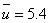m s^-1.

For the error in the mean, we calculate s = 0.47 m s^-1, with N = 5, so σ = 0.21 m s^-1. Thus, the population mean is estimated as 5.40 ± 0.21 m s^-1.